4.3 Information-theoretical security (perfect secrecy)

The historical roots of encryption are in military and diplomatic communications. The first encryption schemes were perhaps invented by the ancient Greeks and Romans. These encryption schemes have survived until today in the form of examples for easily breakable ciphers and can be found in virtually any textbook on cryptography.

Another famous historical example is provided by the Enigma encryption machine, which was used by the Axis powers in World War II. Due to its large key space, this sophisticated rotor-based machine was deemed unbreakable by its inventors. However, building on the work of Polish mathematicians and using (for the time) massive computing power, the Allies were able to prove them wrong 171. Judging from these historical examples, one might get the impression that all encryption schemes can be broken. However, it is possible to devise provably secure encryption schemes.

An encryption scheme that is provably secure even against attackers with unlimited computational capabilities is called perfectly secret (not to be confused with perfect forward secrecy from Chapter 3, A Secret to Share) or information-theoretically secure. In a nutshell, this is achieved by constructing an encryption system that produces ciphertexts which provably – in the sense of mathematical proof – have not enough information for Eve to succeed regardless of her computational and cryptanalytic capabilities. In an example we shall see shortly, the ciphertext provably contains no information about the plaintext at all.

Let’s make this a bit more formal.

An encryption scheme is called perfectly secret if for any probability distribution over ℳ, every message m ∈ℳ, and every ciphertext c ∈𝒞, it holds that:

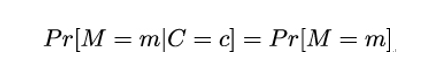
Here, Pr[M = m] is the probability that the plaintext message is m and Pr[M = m|C = c] is the so-called conditional probability that the plaintext message is m given that the corresponding ciphertext observed by Eve is c. This definition was introduced by Claude Shannon, the inventor of Information Theory, in 162.

What does the preceding mathematical definition say? Well, it tells us that Eve’s chances of determining what the plaintext was given the ciphertext c (left-hand side of the definition) are the same if Eve is trying to guess the plaintext without any knowledge of the ciphertext (right-hand side of the definition). In other words, the ciphertext leaks no information whatsoever about the corresponding plaintext in addition to what Eve already knows about the plaintext. For example, Eve might already know that the plaintext is formed by a single bit.

Then her guessing probability is 1/2 and observing c will not improve her chances. Thus, regardless of computational resources at her disposal, the best Eve can do is to guess what the plaintext message was.

In the same report 162, Shannon also provided three criteria that have to be fulfilled so that a symmetric encryption scheme is perfect:

• The plaintext space ℳ must be as large as the cipher space 𝒞 and the keyspace 𝒦
• For every possible m ∈ℳ and every possible c ∈𝒞 there should exist a key k ∈𝒦 such that c = ek(m)
• All keys should occur with equal probability