3.7 Randomness and entropy

In cryptography, the security of most protocols and mechanisms depends on the generation of random sequences of bits or numbers. These sequences must have a sufficient length and be random in a very specific sense: we do not want an attacker to be able to guess part of or the whole sequence. To make this idea more precise, cryptographers use the concept of entropy.

You might be familiar with the notion of entropy from physics. There, entropy is a fundamental property of any complex system and, loosely speaking, describes the tendency of such systems to disorder. As an example, take a gas being injected into a container. At first, the gas particles will still be clustered closely together. But as time passes by, the gas particles will float around and distribute themselves randomly within that container. They do so because the latter configuration offers more possible states (i.e., locations and velocities) for the gas particles; in other words, the entropy of the latter configuration is higher. In that sense, entropy is inevitable in physics because it only increases over time.

3.7.1 Information-theoretic definition of entropy

Cryptography uses the entropy definition from information theory. The information theoretical concept of entropy is defined with the help of random variables.

Let X be a random variable that can take some values x1,x2,…,xn with probability P(X = xi) = pi. Because the pi are probabilities, we must have 0 ≤ pi ≤ 1 for each i and ∑ i=1npi = 1.

Now we can define the entropy of X as

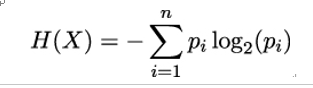
The entropy H(X) can be seen as a mathematical measure of the average amount of information provided by an observation of X [117]. As an example, X could be the outcome of a six-sided die roll. Then, X would take its values from the finite set 1,2,…,6 with probability P(X = x1…6) = 1∕6 and the sum of all possible outcomes ∑ i=16pi being 1. The entropy of X is

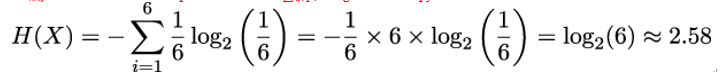
Alternatively, entropy can be viewed as the uncertainty about the outcome before X is observed. This uncertainty is highest if all n outcomes of X are equally likely. In this case, H(X) takes on its maximum value log 2(n).

To illustrate, assume we have an unaltered six-sided die X1 and a manipulated six-sided die X2 that always gives a 3 or a 6 with equal probability. Clearly, the uncertainty of observing X1 – the surprise about the outcome – is larger than that of X2 because we know in advance that X2 will give a 3 or a 6. Indeed,

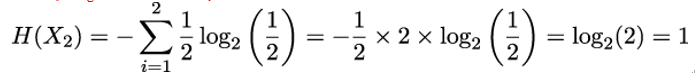
As this example shows, entropy can also be used for approximating the average number of bits required to encode the elements of X. Since the entropy of X1 is 2.58, we need 3 bits to encode them. In contrast, because H(X2) = 1, a single bit is sufficient to encode the outcomes of X2.