4.2 Symmetric cryptosystems

To recap from Chapter 2, Secure Channel and the CIA Triad, confidentiality is achieved using functions fK : ℳ→𝒞 that transform the private information m, also referred to as plaintext, into a scrambled message c = fK(m), referred to as ciphertext. Here, fK is an encryption function. It maps a plaintext m from some larger set ℳ, the plaintext space, to a ciphertext c which, in turn, is an element of some larger set 𝒞, the cipher space.

The functions fK must be bijections, so that we can form the inverse functions, denoted by fK−1, which transform the ciphertexts back to the original plaintexts. The inverse functions are the decryption functions. The bijectivity of the fK also means that ℳ and 𝒞 have the same number of elements.

In order to specify a complete symmetric cryptosystem, we need to define all of its ingredients:

• The plaintext space ℳ and the cipher space 𝒞
• The keyspace 𝒦
• The encryption function fK : ℳ→𝒞
• The decryption function fK−1 : 𝒞→ℳ

Figure 4.5 illustrates the encryption function or encryption operation. The encryption function has two inputs: the plaintext message m ∈ℳ and the secret key K ∈𝒦. They are mapped to the ciphertext c ∈𝒞. For convenience and better readability, it is common in cryptographic literature to use the notation eK for the encryption function instead of the more formal fK. Encryption functions are the fundamental tools of cryptography. In combination with additional cryptographic mechanisms, such as message authentication codes or digital signatures, encryption functions allow Alice and Bob to communicate securely over an unsecured channel. This holds both in the presence of passive as well as active attackers [168].

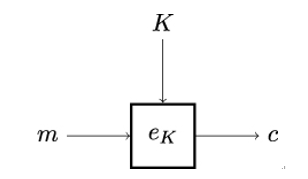
Figure 4.5: Working principle of encryption. The encryption function eK produces the ciphertext c ∈𝒞 from the plaintext message m ∈ℳ and the secret key K ∈𝒦

The decryption function or decryption operation, illustrated in Figure 4.6, is the reverse process. Here, the input is the ciphertext c ∈𝒞 and the secret key k ∈𝒦. The input is mapped back to the original plaintext message m ∈ℳ. Similar to encryption, decryption in cryptographic literature is often denoted as dK instead of the more formal fK−1.

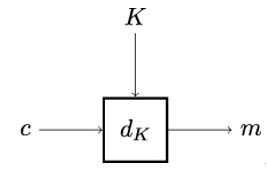
Figure 4.6: Working principle of decryption. The decryption function dK takes as input the ciphertext c ∈𝒞 and the secret key k ∈𝒦, and maps it back to the original plaintext message m ∈ℳ

By taking together the encryption and decryption functions shown here, we can build a symmetric encryption scheme because the same key K is used to both encrypt and decrypt the messages. We will take a look at an example of encryption and decryption shortly.

Encryption functions are oftentimes used as building blocks for other, composite cryptographic mechanisms. These include key establishment schemes, message authentication codes to ensure the authenticity and integrity of messages, as well as protocols for entity authentication.